Maps

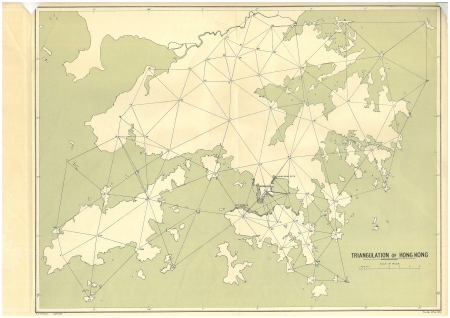
Triangulation of Hong Kong and the New Territories. Adjusted by the G.S.G.S. in 1929-30.

The map comes together with a loose pamphlet, 35pp.

Triangulation of Hong Kong and New Territories

Base – An accepted length derived from some base-extension has been received from the Superintendent of Surveys. This line is that from Partridge Hill to Channel Rock, whereof the length in feet has been given as the antilogarithm of 4.060 8589. This length has been adopted here as the base.

Triangulation – The field measures supplied by the Superintendent cover a practically complete net. Of a fairly high secondary order of accuracy, they have been adjusted by the G.S.,G.S. The adjustment is rigorous except in so far as it has been necessary to split the triangulation into 9 figures. A simultaneous adjustment of the whole would have been justified only if the measures had been of the first order of precision.

Latitude – The origin for latitude is the Royal Observatory at Kau Lung, whose latitude is given as 22  18’ 13” .20 N. The trigonometrical station was 38.4 feet due south of this position---that of the Transit Circle.

Longitude – The longitude adopted is 7h. 36m. 41.25s., or 114  10” 18” .75 E. This was determined in 1924 from simultaneous observations of Bordeaux signals made at Greenwich and Hong Kong.

Azimuth – The azimuth adopted is that given by the Superintendent. The line from Partridge Hill to Channel Rock is thus assumed to have the azimuth 98  12’ 00”, reckoned from North by East. The observations for base and azimuth are not available.

Geographical Co-ordinates – Consequent on the data above, the latitude and longitude have been completed by Mr W.A. Scott. The spheroid employed was the Clarke 1880 (R.G.S. tables).

Rectangular Co-Ordinates – The rectangular co-ordinates are in metres on the “China Grid.” After preliminary computation direct from the geographicals, they were checked by point-to-point working by Mr. Scott, so that it may be taken that the convergence is also correct.

Should it be required to reduce theses c0=ordinates to feet the Clarke relation of the metre/foot is to be employed:-

1 Metre = 3.280 869 33 Feet,

  1 Foot = 0.304 797 265 Metre,

  Log (Metres) = log (Feet) + 9.484 0110 663.

A rare map not in Empson.

Provenance

ex Library of Congress